Chapter 2 — Building Abstractions with Data

1. What is meant by data?

Axiom for pairs: for any objects x and y, if z = (cons x y), then (car z) = x and (cdr z) = y. Any implementation satisfying this axiom can be used:

(define (cons x y)
  (lambda (pick)
    (cond [(= pick 0) x]
          [(= pick 1) y])))

(define (car z) (z 0))
(define (cdr z) (z 1))

Here a procedure is returned by cons that captures the arguments x and y. The procedure is then applied to 0 in car to return the captured x. The same goes for cdr. This style of programming is called message passing.

Message passing explained, by ChatGPT

In SICP, message passing is used as a paradigm for building programs using objects and classes. Objects are defined as independent entities that encapsulate data and behavior, and they communicate with each other by sending messages.

Message passing involves sending a message from one object to another, requesting some action or information. The receiving object then responds to the message based on its internal state and the message's content. This interaction between objects allows for modularity and encapsulation, as objects can be designed to hide their internal details and only expose the necessary interfaces.

The ability to manipulate procedures as objects automatically provides the ability to represent compound data.

Another implementation, taken from Ex 2.4:

(define (cons x y)
  (λ (m) (m x y)))

(define (car z)
  (z (λ (p q) p)))

(define (cdr z)
  (z (λ (p q) q)))

As in Ex 2.5, you can also represent a pair of integers \(a\), \(b\) with \(2^a 3^b\). This representation, however, cannot take other objects.

(define (cons a b)
  (* (expt 2 a) (expt 3 b)))

(define (factor x a)
  (define (iter x n)
    (if (zero? (remainder x a))
        (iter (/ x a) (1+ n))
        n))
  (iter x 0))

(define (car z) (factor z 2))
(define (cdr z) (factor z 3))

(define x (cons 10 20))
(car x)                                 ; 10
(cdr x)                                 ; 20

Rewrite factor using named let:

(define (factor x a)
  (let iter ([x x] [n 0])
    (let ([q (/ x a)])
      (if (integer? q)
          (iter q (+ n 1))
          n))))

(factor x 2)                            ; 10
(factor x 3)                            ; 20

2. Tree structure

(define (atom? x) (not (pair? x)))

(define (count-leaves x)
  (cond [(null? x) 0]                   ; empty tree
        [(atom? x) 1]                   ; leaf
        [else (+ (count-leaves (car x))
                 (count-leaves (cdr x)))]))

(define (reverse x)
  (define (iter x res)
    (if (null? x)
        res
        (iter (cdr x)
              (cons (car x) res))))
  (iter x '()))

(define (reverse l)                     ; using named let
  (let iter ([l l] [res '()])
    (if (null? l)
        res
        (iter (cdr l)
              (cons (car l) res)))))

(reverse '(1 2 3 4))                    ; (4 3 2 1)
(reverse '((1 2) (3 4) (5 6)))          ; ((5 6) (3 4) (1 2))

(define (deep-reverse x)
  (define (iter x result)
    (if (null? x)
        result
        (let ([first (car x)]
              [rest  (cdr x)])
          (iter rest
                (cons (if (pair? first)
                          (deep-reverse first) ; or (iter first '())
                          first)
                      result)))))
  (iter x '()))

(deep-reverse '((1 2) (3 4) (5 6)))     ; ((6 5) (4 3) (2 1))

(define (deep-reverse x)
  (reverse
   (map (lambda (x)
          (if (pair? x)
              (deep-reverse x)
              x))
        x)))

(define (deep-reverse x)
  (if (pair? x)
      (reverse (map deep-reverse x))
      x))

(define (fringe x)                      ; convert tree to list
  (cond [(null? x) '()]
        [(pair? (car x)) (append (fringe (car x))
                                 (fringe (cdr x)))]
        [else (cons (car x) (fringe (cdr x)))]))

(fringe '((1 2) (3 (4 (5))) 6))         ; (1 2 3 4 5 6)

(define (scale-tree tree factor)
  (cond [(null? tree) '()]
        [(atom? tree) (* tree factor)]
        [else (cons (scale-tree (car tree) factor)
                    (scale-tree (cdr tree) factor))]))

(define (scale-tree tree factor)
  (map (lambda (sub-tree)
         (cond [(null? sub-tree) '()]
               [(pair? sub-tree) (scale-tree sub-tree factor)]
               [else (* sub-tree factor)]))
       tree))


(define (square-tree tree)
  (cond [(null? tree) '()]
        [(pair? tree) (cons (square-tree (car tree))
                            (square-tree (cdr tree)))]
        [else (square tree)]))

(define (square-tree tree)
  (map (lambda (sub-tree)
         (cond [(null? sub-tree) '()]
               [(pair? sub-tree) (square-tree sub-tree)]
               [else (square sub-tree)]))
       tree))

(square-tree '(1 (2 (3 4) 5) (6 7)))

(define (tree-map fun tree)
  (cond [(null? tree) '()]
        [(pair? tree) (cons (tree-map fun (car tree))
                            (tree-map fun (cdr tree)))]
        [else (fun tree)]))

(define (tree-map fun tree)
  (map (lambda (sub-tree)
         (cond [(null? sub-tree) '()]
               [(pair? sub-tree) (tree-map fun sub-tree)]
               [else (fun sub-tree)]))
       tree))

3. Sequences as conventional interfaces

(define (filter predicate sequence)
  (if (null? sequence)
      '()
      (let ([first (car sequence)]
            [rest  (cdr sequence)])
        (if (predicate first)
            (cons first
                  (filter predicate rest))
            (filter predicate rest)))))

(filter odd? '(1 2 3 4 5 6))            ; (1 3 5)

(define (accumulate op initial sequence)
  (if (null? sequence)
      initial
      (op (car sequence)
          (accumulate op initial (cdr sequence)))))

(accumulate * 1 '(1 2 3 4 5))           ; 120
(accumulate cons '() '(1 2 3 4 5))      ; (1 2 3 4 5)

(define (map f sequence)
  (accumulate (lambda (first rest)
                (cons (f first)
                      rest))
              '()
              sequence))

(map 1+ '(1 2 3))                       ; (2 3 4)

(define (append s1 s2)
  (accumulate cons s2 s1))

(append '(1 2 3) '(4 5 6))              ; (1 2 3 4 5 6)

(define (length s)
  (accumulate (lambda (_ c)
                (1+ c))
              0 s))

(length '(1 2 3))                       ; 3

(define (enumerate-interval low high)
  (if (> low high)
      '()
      (cons low
            (enumerate-interval (+ low 1) high))))

(enumerate-interval 2 7)                ; (2 3 4 5 6 7)

(define (enumerate-tree tree)
  (cond [(null? tree) '()]
        [(atom? tree) (list tree)]
        [else (append (enumerate-tree (car tree))
                      (enumerate-tree (cdr tree)))]))

(enumerate-tree '(1 (2 (3 4)) 5))       ; (1 2 3 4 5)


(define (sum-odd-squares tree)
  (accumulate + 0
              (map square
                   (filter odd?
                           (enumerate-tree tree)))))

(define (even-fibs n)
  (accumulate cons '()
              (filter even?
                      (map fib
                           (enumerate-interval 0 n)))))

(define (salary-of-highest-paid-programmer records)
  (accumulate max 0
              (map salary
                   (filter programmer? records))))

4. Folding left & right

Both fold-left and fold-right takes

op: a procedure with two arguments
initial: the initial value
sequence: the sequence to be accumulated/folded.

(define (fold-left op initial sequence)
  (define (iter result rest)
    (if (null? rest)
        result
        (iter (op result (car rest))
              (cdr rest))))
  (iter initial sequence))

(define (fold-right op initial sequence)
  (if (null? sequence)
      initial
      (op (car sequence)
          (fold-right op initial (cdr sequence)))))

But they apply op in different directions. fold-left folds from left to right, calls (op running-sum current-value). fold-right folds from right to left, calls (op current-value running-sum).

For operators that satisfy transitivity, the result is the same, but for others such as division and cons, the results are different.

(fold-left / 1 '(1 2 3))                ; (((1 / 1) / 2) / 3) -> 1/6
(fold-right / 1 '(1 2 3))               ; (1 / (2 / (3 / 1))) -> 3/2

You can implement reverse using either, but with different op:

(define (reverse sequence)
  (fold-left (lambda (sum cur)
               (cons cur sum))
             '()
             sequence))

(define (reverse sequence)
  (fold-right (lambda (cur sum)
                (append sum (list cur)))
              '()
              sequence))

5. Functional geometry

See this repo.

6. Symbolic differentiation

I've chosen my representation to be the same as the representation in my language.

Note the use of quotes ('). We're talking about the symbol + and *, instead of the procedures they represent.

(define (atom? exp)
  (not (pair? exp)))

(define (constant? exp var)
  ;; whether the expression (exp) is a constant
  ;; with respect to the variable (var)
  (and [atom? exp]
       [not (eq? exp var)]))

(define (same-var? exp var)
  (and [atom? exp]
       [eq? exp var]))

(define (sum? exp)
  (and [pair? exp]
       [eq? (car exp) '+]))

(define (make-sum a1 a2)
  (cond [(and (number? a1) (number? a2)) (+ a1 a2)]
        [(and (number? a1) (zero? a1)) a2]
        [(and (number? a2) (zero? a2)) a1]
        [else (list '+ a1 a2)]))

(define (a1 exp) (cadr exp))
(define (a2 exp) (caddr exp))

(define (product? exp)
  (and [pair? exp]
       [eq? (car exp) '*]))

(define (make-product m1 m2)
  (cond [(and (number? m1) (number? m2)) (* m1 m2)]
        [(and (number? m1) (= m1 1)) m2]
        [(and (number? m2) (= m2 1)) m1]
        [(or (and (number? m1) (zero? m1))
             (and (number? m2) (zero? m2))) 0]
        [else (list '* m1 m2)]))

(define (m1 exp) (cadr exp))
(define (m2 exp) (caddr exp))

(define (deriv exp var)
  (cond [(constant? exp var) 0]
        [(same-var? exp var) 1]
        [(sum? exp)
         (make-sum (deriv (a1 exp) var)
                   (deriv (a2 exp) var))]
        [(product? exp)
         (make-sum (make-product (m1 exp) (deriv (m2 exp) var))
                   (make-product (m2 exp) (deriv (m1 exp) var)))]))


(define foo '(+ (* a (* x x))           ; ax^2 + bx + c
                (+ (* b x)
                   c)))

(deriv foo 'x)
;;; original:
;; => (+ (+ (* a (+ (* x 1) (* x 1)))
;;          (* (* x x) 0))
;;       (+ (+ (* b 1) (* x 0))
;;          0))
;;; updated make-sum & make-product
;; => (+ (* a (+ x x)) b)

This representation, however, does not allow arbitrary numbers of terms for + and *.

(deriv '(+ x x x x) 'x)                 ; 2
(deriv '(* x x x) 'x)                   ; (+ x x)

To incorporate multiple terms while not changing deriv, we just need to change the representation. a2 will now check the number of arguments of the expression. If only two, then return the second one as usual. a2 will make another sum expression if there are more than two arguments. The same is true for m2.

(define (a2 exp)
  (if (null? (cdddr exp))
      (caddr exp)
      (cons '+ (cddr exp))))

(define (m2 exp)
  (if (null? (cdddr exp))
      (caddr exp)
      (cons '* (cddr exp))))

(deriv '(+ x x x x) 'x)                 ; 4
(deriv '(* x x x) 'x)                   ; (+ (* x (+ x x)) (* x x))

7. TODO Pattern matching and rule-based substitution

From MIT 6.001 SICP Video Lectures 4A.

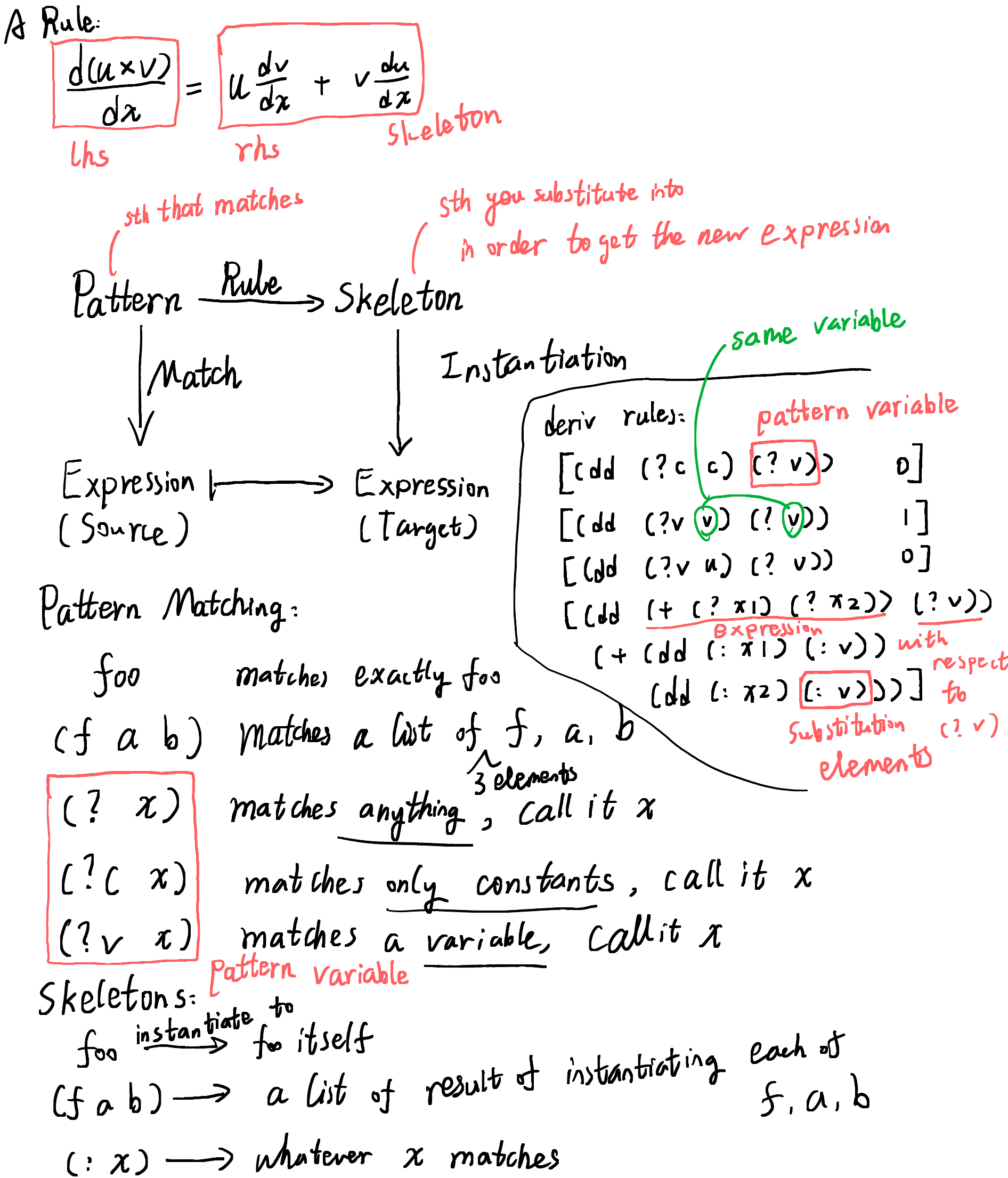
Think about the differentiation process in terms of pattern matching & substitution. A differentiation rule such as \[ \frac{\mathrm{d} (u \times v)}{\mathrm{d} x} = u \frac{\mathrm{d} v}{\mathrm{d} x} + v \frac{\mathrm{d} u}{\mathrm{d} x}\] has a left hand side (LHS) called pattern and a right hand side (RHS) called skeleton.

If a particular source expression matches that pattern, for example \(\frac{\mathrm{d} (x \times y)}{\mathrm{d} x}\), then by applying the rule to the expression, we instantiate the skeleton to the resulting target expression: \(x \frac{\mathrm{d} y}{\mathrm{d} x} + y \frac{\mathrm{d} x}{\mathrm{d} x}\).

In order to implement this pattern matching language in Lisp, we define some patterns:

foo matches exactly the symbol foo
(f a b) matches a list of three patterns: f, a, b
(? x) matches anything, and calls it x
(?c x) matches only constants, and calls it x
(?v x) matches a variable, and calls it x.

and a few skeletons:

foo instantiates to foo itself
(f a b) instantiates to a list of three elements, each the instantiation of f, a, b
(: x) instantiates to whatever x matches.

(? x), (?c x) and (?v x) are pattern variables.

Each rule has the form of a list with two elements—a pattern and a skeleton. The derivative of exp with respect to var is in the form of (dd exp var). The derivation rules can thus be defined as:

(define deriv-rules
  '([(dd (?c c) (? v)) 0]
    [(dd (?v v) (? v)) 1]
    [(dd (?v u) (? v)) 0]

    [(dd (+ (? x1) (? x2)) (? v))
     (+ (dd (: x1) (: v))
        (dd (: x2) (: v)))]

    [(dd (* (? x1) (? x2)) (? v))
     (+ [* (: x1) (dd (: x2) (: v))]
        [* (dd (: x1) (: v)) (: x2)])]))

7.1. Implementation

The whole idea is to have a simplifier that knows a set of rules, so that given an expression, it will produce a most simplified version based on the rules.

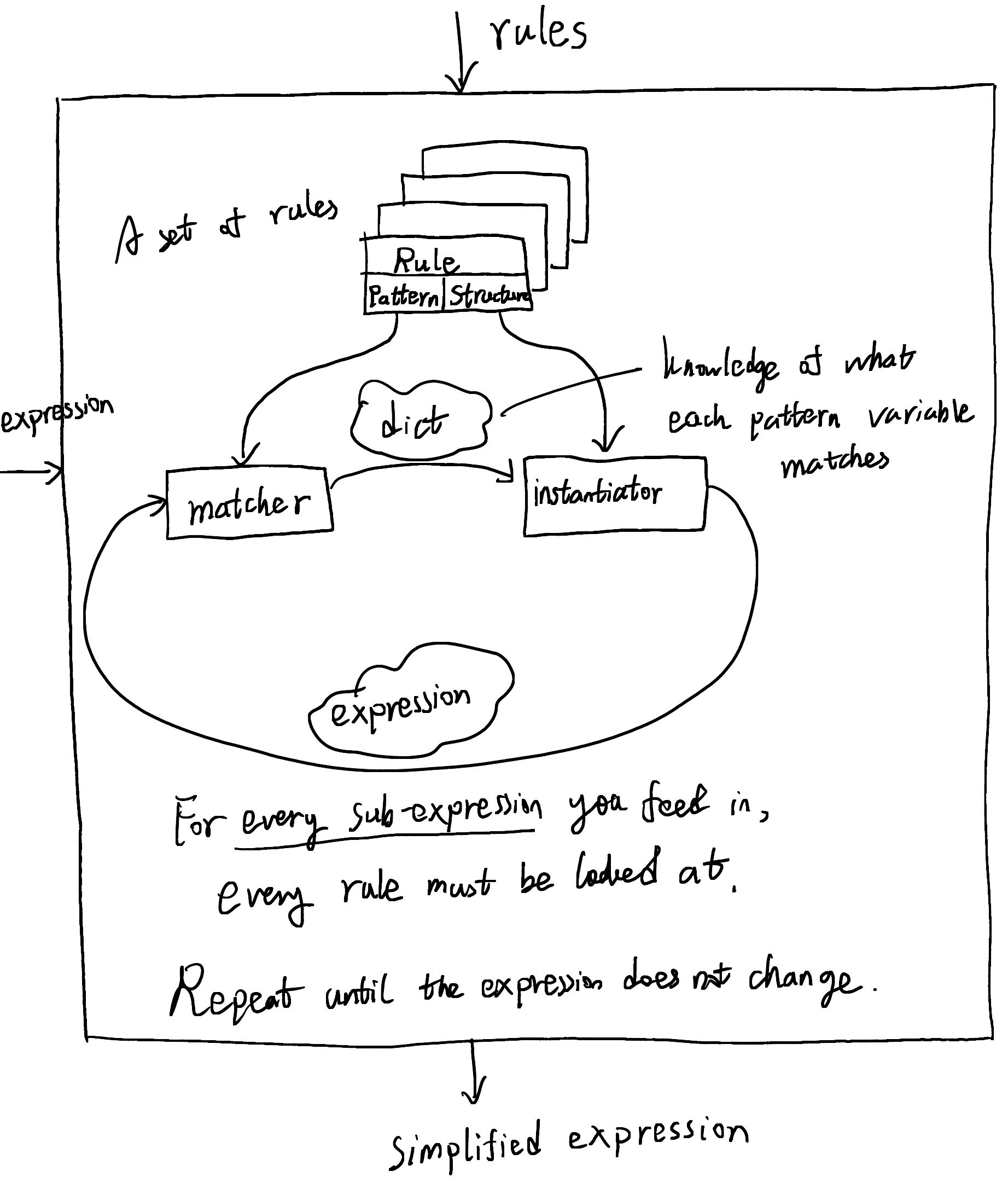
As in Fig. 2, the simplifier takes an expression and a set of rules. It is made up of a matcher and an instantiator. For every sub-expression, the matcher traverses all the patterns, and for each pattern, it creates a dictionary of the mapping of pattern variables and the expressions they match. The simplifier then pass each dictionary to the instantiator, so the latter can instantiate the skeleton according to the dictionary, thus producing a simplified expression.

Think of the expression as a tree whose each node is a sub-expression. The whole process is then a depth first search of all the nodes. It applies each rule to the sub-expression until it cannot be simplified any further, then it goes on to the next sub-expression. The whole process stops when the root expression does not change.

7.1.1. Matcher

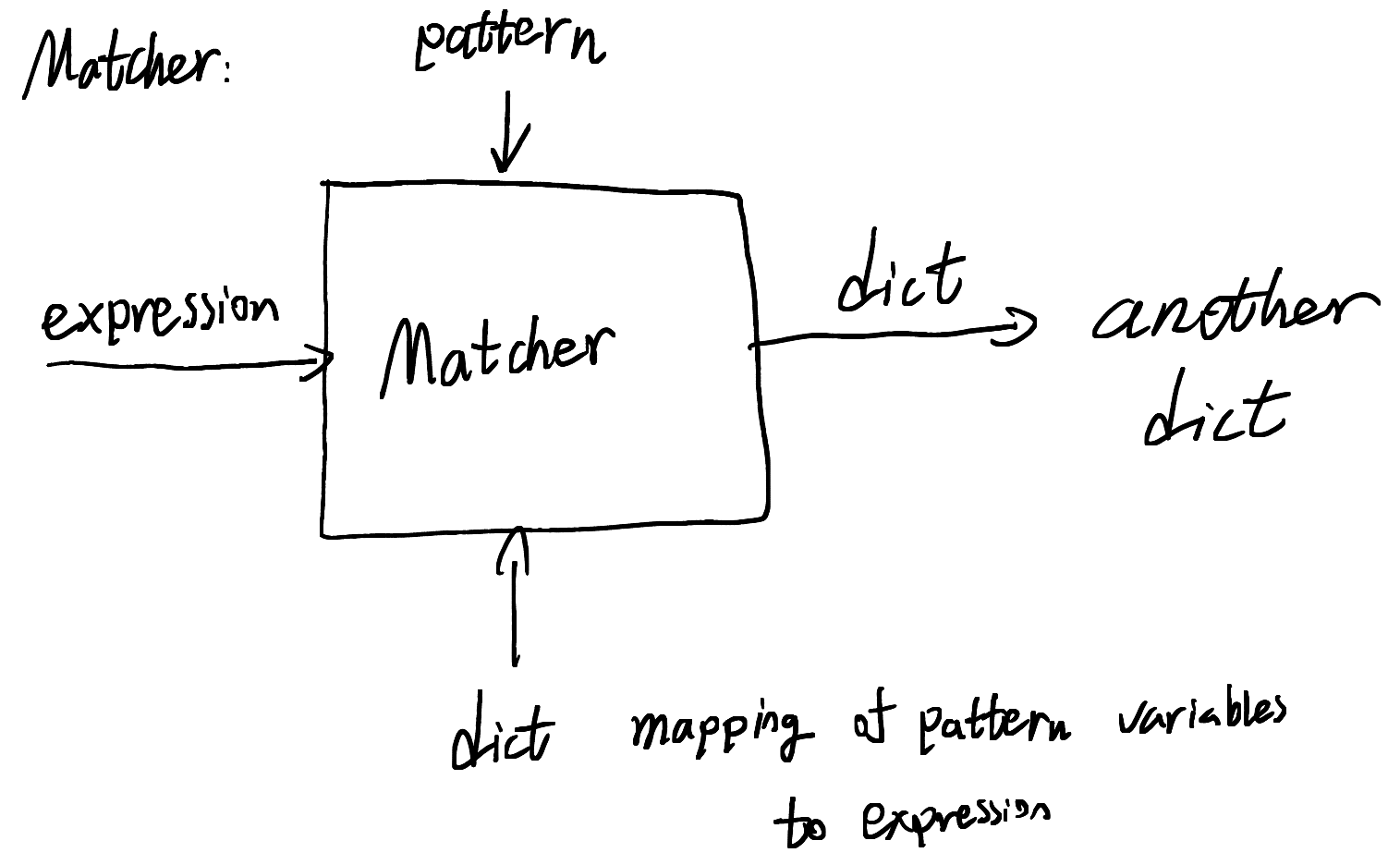
The matcher takes an expression, a pttern and a dictionary, then returns another dictionary. It needs to traverse the pattern tree and the expression at the same time to ensure the two matches. Along the way it constructs the dictionary.

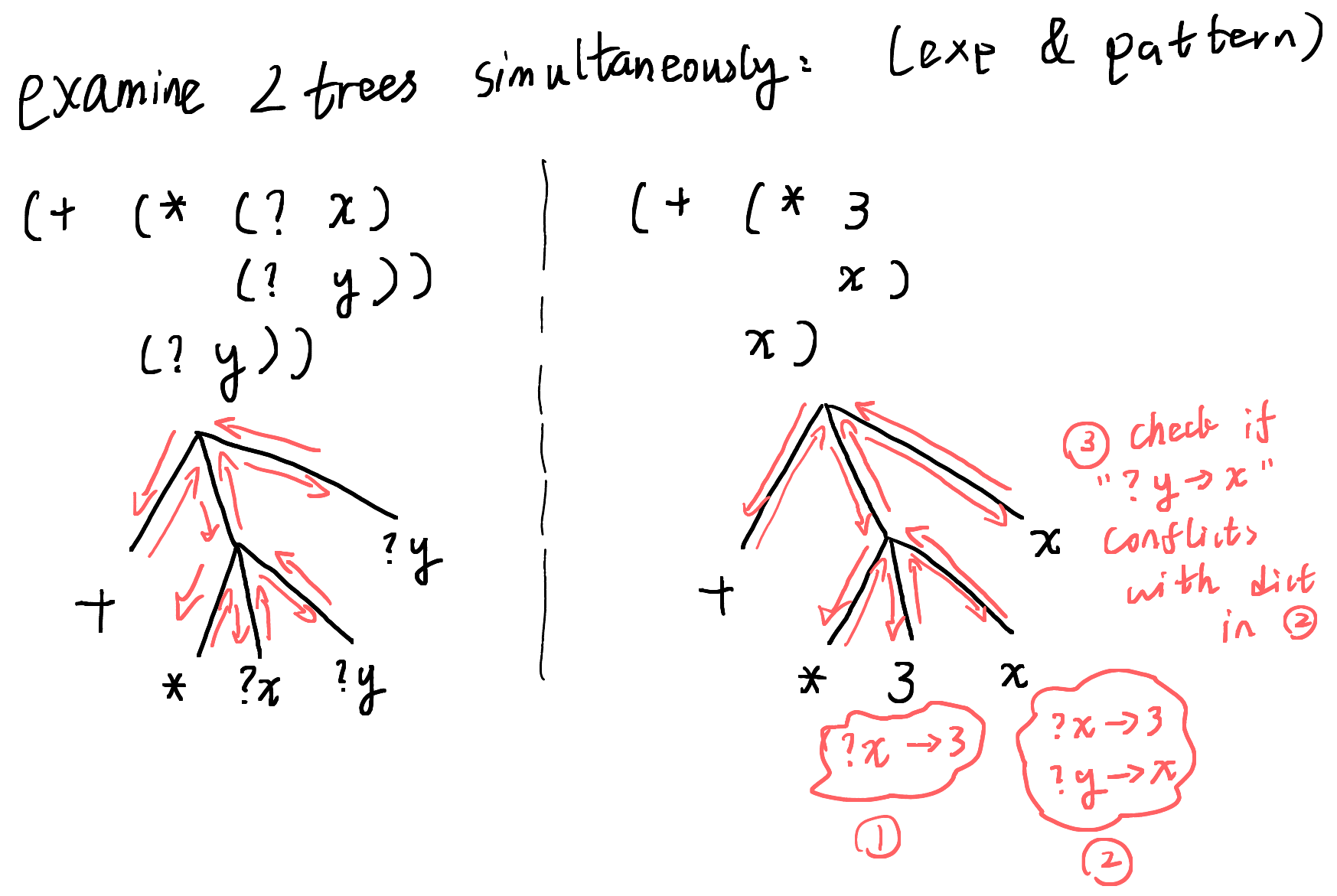
If the expression tree does not match the pattern, then there's a conflict, the dict becomes 'failed:

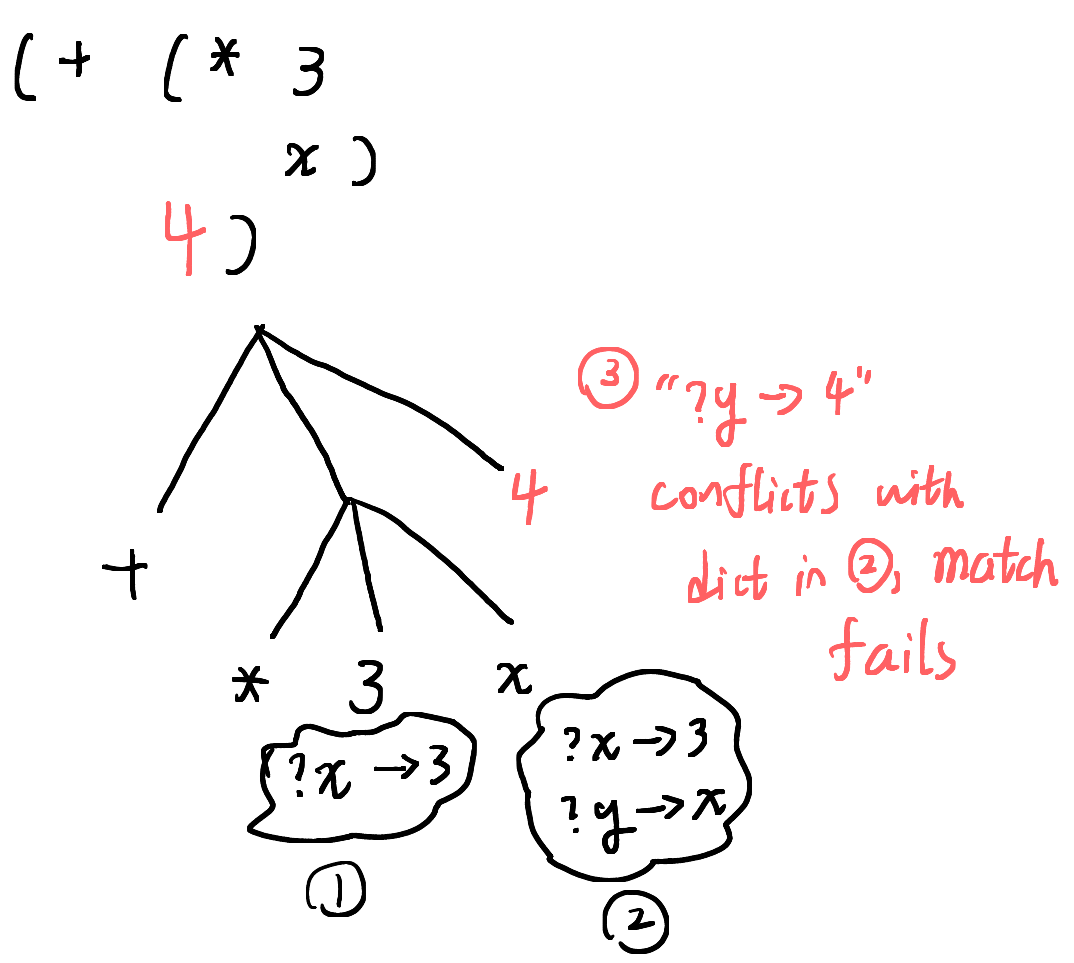
(define (match pat exp dict)
  (cond [(eq? dict 'failed) 'failed]
        [(atom? pat)
         (if (and (atom? exp) (eq? pat exp))
             dict   ; pat & exp are the same atom, mach success, dict
                                        ; does not change. e.g. foo -> foo, * -> *, + -> +
             'failed)]
        [(arbitrary-constant? pat)      ; (?c v)
         (if (constant? exp)
             (extend-dict pat exp dict) ; first check for conflicts, then extend
             'failed)]
        [(arbitrary-variable? pat)      ; (?v v)
         (if (variable? exp)
             (extend-dict pat exp dict)
             'failed)]
        [(arbitrary-expression? pat)    ; (? v)
         (extend-dict pat exp dict)]
        ;; pattern is not atom, but expression is, then match fails
        [(atom? exp) 'failed]
        [else (match (cdr pat)
                     (cdr exp)
                     (match (car pat)
                            (car exp)
                            dict))]))

7.1.2. Instantiater

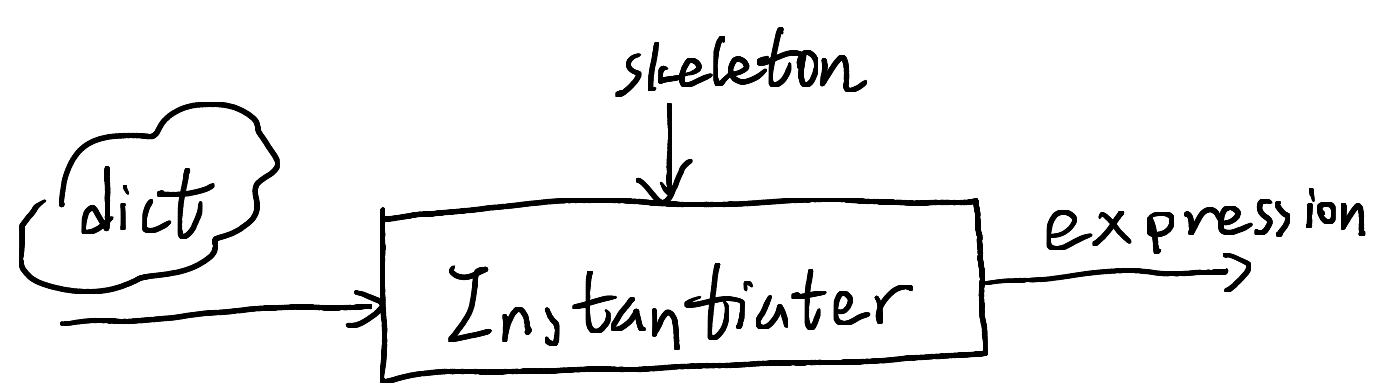
The instantiator takes a dictionary and a skeleton, and instantiate the skeleton to the resulting expression.

(define (instantiate skeleton dict)
  (define (loop s)
    (cond [(atom? s) s]
          [(skeleton-evaluation? s)     ; (: v)
           ;; (eval-exp '(: e1 e2 ...)) => (e1 e2 ...)
           (evaluate (eval-exp s) dict)]
          [else (cons (loop (car s))
                      (loop (cdr s)))]))
  (loop skeleton))

(define (evaluate form dict)
  (if (atom? form)
      (lookup form dict)
      (apply
       (eval (lookup (car form) dict) ; operator
             user-initial-environment)
       (mapcar (lambda (v)            ; operands
                 (lookup v dict))
               (cdr form)))))

7.1.3. Simplifier

A simplifier takes as argument a set of rules, and returns a procedure that simplifies expressions.

(define (simplifier the-rules)
  ;; returns a procedure that simplifies expressions
  ;; ;; [1] uses two procedures to simplify
  ;; (define (simplify-exp exp)
  ;;   (try-rules (if (compound? exp)
  ;;                  (simplify-parts exp)
  ;;                  exp)))
  ;; (define (simplify-parts exp)
  ;;   (if (null? exp)
  ;;       '()
  ;;       (cons (simplify-exp (car exp))
  ;;             (simplify-exp (cdr exp)))))
  ;; [2] using only one procedure
  (define (simplify-exp exp)
    (try-rules (if (compound? exp)
                   (map simplify-exp exp)
                   exp)))

  (define (try-rules exp)
    (define (scan rules)
      (if (null? rules)
          exp
          (let ([dict
                 (match (pattern (car rules))
                        exp
                        (empty-dictionary))])
            (if (eq? dict 'failed)
                (scan (cdr rules))
                (simplify-exp
                 (instantiate
                  (skeleton (car rules))
                  dict))))))
    (scan the-rules))
  simplify-exp)

Use simplifier to create a differenation function:

(define dsimp
  (simplifier deriv-rules))

(dsimp '(dd (+ x y) x))                 ; => (+ 1 0)

7.1.4. Pattern & Skeleton

;;; the variable name of a pattern
;;; (variable-name '(?c exp)) => exp
(define (variable-name pattern)
  (cadr pattern))

7.1.5. Dictionary

A dictionary is implemented as an alist of mappings.

;;; construct an empty dictionary (alist)
(define (empty-dictionary) '())

;;; extent the dictionary by adding to it the knowledge that pattern
;;; matches data.
;;; It first looks for the pattern in dict, if not found, then simply
;;; add to the dict.  If found, then check for conflict.
(define (extend-dictionary pattern dat dict)
  (let* ([name (variable-name pattern)]
         [v (assq name dict)])
    (cond [(null? v)                    ; pattern not found
           (cons (list name dat) dict)]
          ;; pattern found, check for conflict
          [(eq? (cadr v) dat) dict]     ; no conflict
          [else 'failed])))             ; different than before

;;; look up meaning of variables in the dict
(define (lookup var dict)
  (let ([v (assq var dict)])
    (if (null? v) var (cadr v))))

8. Flatmap

To produce a list of ordered pairs \((i, j)\) s.t. \(1 \le i \le j \le n\), first we nest two maps:

(let ([n 3])
  (map (lambda (i)
         (map (lambda (j) (list i j))
              (enumerate-interval i n)))
       (enumerate-interval 1 n)))
;; (((1 1) (1 2) (1 3))
;;  ((2 2) (2 3))
;;  ((3 3)))

The result is a list of lists. Use accumulate on the outer list to flatten it:

(let ([n 3])
  (accumulate append '()
              (map (lambda (i)
                     (map (lambda (j) (list i j))
                          (enumerate-interval i n)))
                   (enumerate-interval 1 n))))
;; ((1 1) (1 2) (1 3) (2 2) (2 3) (3 3))

The combination of mapping and accumulating with append is so common in this sort of program that we will isolate it as a separate procedure:

(define (flatmap proc seq)
  (accumulate append '()
              (map proc seq)))

Then we can define ordered pairs and even ordered triplets:

(define (ordered-pairs n)
  (flatmap (lambda (i)
             (map (lambda (j) (list i j))
                  (enumerate-interval 1 n)))
           (enumerate-interval 1 n)))

(ordered-pairs 3)
;; ((1 1) (1 2) (1 3) (2 1) (2 2) (2 3) (3 1) (3 2) (3 3))

(define (ordered-triplets n)
  (flatmap (lambda (x)
             (map (lambda (l) (cons x l))
                  (ordered-pairs n)))
           (enumerate-interval 1 n)))

(ordered-triplets 2)
;; ((1 1 1) (1 1 2) (1 2 1) (1 2 2) (2 1 1) (2 1 2) (2 2 1) (2 2 2))

9. List as tree as set

Implement an ordered set of numbers using binary search tree. A tree is a list of 3 elements—an entry in the set, its left branch, and right branch.

(define (entry tree) (car tree))          ; first
(define (left-branch tree) (cadr tree))   ; second
(define (right-branch tree) (caddr tree)) ; third
(define (make-tree entry left right)
  (list entry left right))

Finding an element of a balanced tree takes \(O(\log n)\) time.

(define (element-of-set? x set)
  (cond [(null? set) #f]
        [(= x (entry set)) #t]
        [(> x (entry set)) (element-of-set? x (left-branch set))]
        [else (element-of-set? x (right-branch set))]))

adjoin-set inserts entry x to tree set:

(define (adjoin-set x set)
  (cond [(null? set) (make-tree x '() '())]
        [(= x (entry set)) set]         ; already in the set
        [(> x (entry set))              ; insert to left branch
         (make-tree (entry set)
                    (adjoin-set x (left-branch set))
                    (right-branch set))]
        [else                           ; insert to right branch
         (make-tree (entry set)
                    (left-branch set)
                    (adjoin-set x (right-branch set)))]))

Flattening a tree into list using inorder traversal:

;;; [1] append makes this slower than [2]
(define (tree->list-1 tree)
  (if (null? tree)
      '()
      (append (tree->list-1 (left-branch tree))
              (cons (entry tree)
                    (tree->list-1 (right-branch tree))))))
;;; [2]
(define (tree->list-2 tree)
  (define (copy-to-list tree result-list)
    (if (null? tree)
        result-list
        (copy-to-list (left-branch tree)
                      (cons (entry tree)
                            (copy-to-list (right-branch tree)
                                          result-list)))))
  (copy-to-list tree '()))

(define tree (make-tree 7
                        (make-tree 3
                                   (make-tree 1 '() '())
                                   (make-tree 5 '() '()))
                        (make-tree 9
                                   '()
                                   (make-tree 11 '() '()))))

(tree->list-1 tree)                     ; (1 3 5 7 9 11)
(tree->list-2 tree)                     ; (1 3 5 7 9 11)

Converting an ordered list to a balanced tree: (Ex 2.64)

The following procedure list->tree converts an ordered list to a balanced binary tree. The helper procedure partial-tree takes as arguments an integer \(n\) and list of at least \(n\) elements and constructs a balanced tree containing the first \(n\) elements of the list. The result returned by partial-tree is a pair (formed with cons) whose car is the constructed tree and whose cdr is the list of elements not included in the tree.

(define (list->tree l)
  (define (partial-tree elts n)
    (if (= n 0)
        (cons '() elts)                 ; an empty tree & (rest of) the list
        (let* ([left-size (quotient (- n 1) 2)]
               [right-size (- n left-size 1)]
               [left-result (partial-tree elts left-size)]
               [left-tree (car left-result)]
               [non-left-elts (cdr left-result)]
               [this-entry (car non-left-elts)]
               [right-elts (cdr non-left-elts)]
               [right-result (partial-tree right-elts right-size)]
               [right-tree (car right-result)]
               [remaining-elts (cdr right-result)])
          (cons (make-tree this-entry
                           left-tree
                           right-tree)
                remaining-elts))))
  (car (partial-tree l (length l))))

(tree->list-1 (list->tree '(1 2 3 4)))  ; (1 2 3 4)

10. Huffman encoding tree

In a huffman tree, a node is either a general tree, or a leaf. In the following code, node refers to either a general tree or a leaf, leaf refers specifically to a leaf, and tree a general tree.

A leaf is represented by a list consisting of the symbol leaf, the symbol at the leaf, and its weight.

(define (make-leaf symbol weight)
  (list 'leaf symbol weight))
(define (leaf? node) (eq? (car node) 'leaf))
(define (symbol-leaf leaf) (cadr leaf))
(define (weight-leaf leaf) (caddr leaf))

A general tree is a list of a left branch, a right branch, a set of symbols, and a weight. The procedures symbols and weight must do something slightly different depending on whether they are called with a leaf or a general tree.

(define (make-code-tree left right)
  (list left
        right
        (append (symbols left) (symbols right))
        (+ (weight left) (weight right))))
(define (left-branch tree) (car tree))
(define (right-branch tree) (cadr tree))
(define (symbols node)
  (if (leaf? node)
      (list (symbol-leaf node))
      (caddr node)))
(define (weight node)
  (if (leaf? node)
      (weight-leaf node)
      (cadddr node)))

The decode process is not hard. It takes bits (a list of 0's and 1's) and the Huffman tree. At each run, if

node is a leaf, it means the bit just processed ends a symbol, and the remaining bits can either be empty [2], or represent yet more symbols [3,4]. So we cons that symbol to the result, and restart at the root of the tree.
node is not a leaf and bits is empty, then the decode process ends.
the bit is 0, then go to the left branch.
the bit is 1, then go to the right branch.
the bit is neither 0 or 1, there's a bad bit in bits.

(define (decode bits tree)
  (define (run bits node)
    (cond [(leaf? node) (cons (symbol-leaf node) (run bits tree))] ; [1]
          [(null? bits) '()]                                       ; [2]
          [(= (car bits) 0) (run (cdr bits) (left-branch node))]   ; [3]
          [(= (car bits) 1) (run (cdr bits) (right-branch node))]  ; [4]
          [else (error "bad bit in DECODE" (car bits))]))          ; [5]
  (run bits tree))

Example of decode:

(define sample-tree
  (make-code-tree (make-leaf 'A 4)
                  (make-code-tree (make-leaf 'B 2)
                                  (make-code-tree (make-leaf 'D 1)
                                                  (make-leaf 'C 1)))))

(define sample-bits '(0 1 1 0 0 1 0 1 0 1 1 1 0))
(define sample-message '(A D A B B C A))

(equal? (decode sample-bits sample-tree) sample-message) ; #t

The encode process:

(define (encode msg tree)
  (define (encode-symbol symbol node)
    (if (leaf? node)
        '()
        (let ([left (left-branch node)]
              [right (right-branch node)])
          (cond [(memq symbol (symbols left))
                 (cons 0 (encode-symbol symbol left))]
                [(memq symbol (symbols right))
                 (cons 1 (encode-symbol symbol right))]
                [else (error "Symbol not in tree:" symbol)]))))
  (if (null? msg)
      '()
      (append (encode-symbol (car msg) tree)
              (encode (cdr msg) tree))))

(equal? (encode sample-message sample-tree) sample-bits) ; #t

In building the Huffman tree, the symbol-frequency pairs are given where all the symbols are unique. The pairs are first converted by make-leaf-set to an ordered set (list) of leaves, and then merged to the final tree (which we'll talk later). adjoin-set adds node (note this is a node, not just a leaf) to an ordered list set. It assumes node is never in set.

;;; This is defined later.
;; (define (generate-huffman-tree pairs)
;;   (successive-merge (make-leaf-set pairs)))

(define (adjoin-set node set)
  (cond [(null? set) (list node)]
        [(< (weight node) (weight (car set))) (cons node set)]
        [else (cons (car set)
                    (adjoin-set node (cdr set)))]))

(define (make-leaf-set pairs)
  (if (null? pairs)
      '()
      (let ([pair (car pairs)]
            [rest (cdr pairs)])
        (adjoin-set (make-leaf (car pair) (cadr pair))
                    (make-leaf-set rest)))))

(define sample-pairs '((A 4) (B 2) (C 1) (D 1)))
(make-leaf-set sample-pairs)
;; ((leaf D 1) (leaf C 1) (leaf B 2) (leaf A 4))

successive-merge uses make-code-tree to successively merge the smallest-weight elements of the set until there's only one element left. The ordered set originally contains only leaves, but the leaves are merged to become general tree nodes.

(define (generate-huffman-tree pairs)
  (define (successive-merge set)
    (if (null? (cdr set))
        (car set)                 ; only one element left, it's the tree
        (let ([first (car set)]
              [second (cadr set)]
              [rest (cddr set)])
          (successive-merge
           (adjoin-set (make-code-tree first second) ; merge first & second
                       rest)))))                     ; and join with rest
  (successive-merge (make-leaf-set pairs)))

(generate-huffman-tree sample-pairs)
;; ((leaf A 4)
;;  ((leaf B 2)
;;   ((leaf D 1) (leaf C 1) (D C) 2)
;;   (B D C)
;;   4)
;;  (A B D C)
;;  8)

(let ([tree (generate-huffman-tree sample-pairs)])
  (and (equal? (encode sample-message tree) sample-bits)
       (equal? (decode sample-bits tree) sample-message))) ; #t

11. Generic operations

A complex number \(z = x + i y = r \, e^{i A}\) can be represented in either rectangular form as \((x, y)\) or in polar form as \((r, A)\). Both form can be implemented with a cons pair.

We get \(x\) and \(y\) with real-part and imag-part.
We get \(r\) and \(A\) with magnitude and angle.
We construct a complex number using \((x, y)\) or \((r, A)\) with make-from-real-imag and make-from-mag-ang.

Axiom for the six functions:

(make-from-real-imag (real-part z) (imag-part z)) is equal to z
(make-from-mag-ang (magnitude z) (angle z))       is equal to z

Assuming we have implemented the six functions, we can use them to do complex arithmetic.

(define (add-complex z1 z2)
  (make-from-real-imag (+ (real-part z1) (real-part z2))
                       (+ (imag-part z1) (imag-part z2))))

(define (sub-complex z1 z2)
  (make-from-real-imag (- (real-part z1) (real-part z2))
                       (- (imag-part z1) (imag-part z2))))

(define (mul-complex z1 z2)
  (make-from-mag-ang (* (magnitude z1) (magnitude z2))
                     (+ (angle z1) (angle z2))))

(define (div-complex z1 z2)
  (make-from-mag-ang (/ (magnitude z1) (magnitude z2))
                     (- (angle z1) (angle z2))))

The resulting complex-number system has the structure shown below.

11.1. Implementation

We convert each pair into a tagged datum by attaching a type tag ('rectangular or 'polar) in front of the pair so as not to confuse one form with another. A tagged datum is a cons pair of the type tag and its content.

(define (attach-tag type-tag content)
  (cons type-tag content))
(define (type-tag datum)
  (if (pair? datum)
      (car datum)
      (error "Bad tagged datum: TYPE-TAG" datum)))
(define (content datum)
  (if (pair? datum)
      (cdr datum)
      (error "Bad tagged datum: CONTENT" datum)))

By checking the type tag, we can distinguish from the two representations:

(define (rectangular? z)
  (eq? (type-tag z) 'rectangular))
(define (polar? z)
  (eq? (type-tag z) 'polar))

We add the suffix -rectangular or -polar to the above 6 functions to distinguish on which form the procedure is operating on (or is constructing).

(define (square x) (* x x))

(define (real-part-rectangular z) (car z))
(define (imag-part-rectangular z) (cdr z))
(define (magnitude-rectangular z)
  (sqrt (+ (square (real-part-rectangular z))
           (square (imag-part-rectangular z)))))
(define (angle-rectangular z)
  (atan (imag-part-rectangular z)
        (real-part-rectangular z)))
(define (make-from-real-imag-rectangular x y)
  (attach-tag 'rectangular (cons x y)))
(define (make-from-mag-ang-rectangular r a)
  (attach-tag 'rectangular
              (cons (* r (cos a)) (* r (sin a)))))

(define (real-part-polar z)
  (* (magnitude-polar z) (cos (angle-polar z))))
(define (imag-part-polar z)
  (* (magnitude-polar z) (sin (angle-polar z))))
(define (magnitude-polar z) (car z))
(define (angle-polar z) (cdr z))
(define (make-from-real-imag-polar x y)
  (attach-tag 'polar
              (cons (sqrt (+ (square x) (square y)))
                    (atan y x))))
(define (make-from-mag-ang-polar r a)
  (attach-tag 'polar (cons r a)))

The above functions (excepting constructors) can be organized into an operation-type table, where the rows represent operations and the columns represent different types (representations).

To combine different types and operations, we have three choices:

dispatch on data types: have the function decide what to do depending on the data type given. This is called explicit dispatch.
dispatch on operation names: have the object decide what to do depending on the name of the operation given. This style of programming is called message passing.
dispatch on both: have only one general procedure that decides what to do depending on both the type of data and name of operation. This is called data-directed programming.

The key idea of data-directed programming is to handle generic operations in programs by dealing explicitly with operation-and-type tables. The style of programming we used in Section 2.4.2 (dispatch on data types) organized the required dispatching on type by having each operation take care of its own dispatching. In effect, this decomposes the operation-and-type table into rows, with each generic operation procedure representing a row of the table.

An alternative implementation strategy is to decompose the table into columns and, instead of using "intelligent operations" that dispatch on data types, to work with "intelligent data objects" that dispatch on operation names. We can do this by arranging things so that a data object, such as a rectangular number, is represented as a procedure that takes as input the required operation name and performs the operation indicated.

11.2. Dispatch on data types

Let each general procedure operate on the complex number z depending on the type of z:

(define (real-part z)
  (cond [(rectangular? z) (real-part-rectangular (contents z))]
        [(polar? z) (real-part-polar (contents z))]
        [else (error "Unknown type: REAL-PART" z)]))
(define (imag-part z)
  (cond [(rectangular? z) (imag-part-rectangular (contents z))]
        [(polar? z) (imag-part-polar (contents z))]
        [else (error "Unknown type: IMAG-PART" z)]))
(define (magnitude z)
  (cond [(rectangular? z) (magnitude-rectangular (contents z))]
        [(polar? z) (magnitude-polar (contents z))]
        [else (error "Unknown type: MAGNITUDE" z)]))
(define (angle z)
  (cond [(rectangular? z) (angle-rectangular (contents z))]
        [(polar? z) (angle-polar (contents z))]
        [else (error "Unknown type: ANGLE" z)]))
(define (make-from-real-imag x y)
  (make-from-real-imag-rectangular x y))
(define (make-from-mag-ang r a)
  (make-from-mag-ang-polar r a))

This approach, however, is not additive—code has to change each time a new type is added.

The person implementing the generic selector procedures must modify those procedures each time a new representation is installed, and the people interfacing the individual representations must modify their code to avoid name conflicts.

11.3. Dispatch on operation names

Message passing represents an object with a procedure that takes as input the required operation name and perform the operation indicated.

(define (make-from-real-imag x y)
  (lambda (op)
    (cond [(eq? op 'real-part) x]
          [(eq? op 'imag-part) y]
          [(eq? op 'magnitude) (sqrt (+ (* x x) (* y y)))]
          [(eq? op 'angle) (atan y x)]
          [else (error "Unknown op: MAKE-FROM-REAL-IMAG" op)])))

(define (make-from-mag-ang r a)
  (lambda (op)
    (cond [(eq? op 'real-part) (* r (cos a))]
          [(eq? op 'imag-part) (* r (sin a))]
          [(eq? op 'magnitude) r]
          [(eq? op 'angle) a]
          [else (error "Unknown op: MAKE-FROM-MAG-ANG" op)])))

This technique is also used in the make-stack and make-queue procedures in Chapter 2 of TSPL4.

11.4. Dispatch on both

In dispatching on data type, the interfaces were 6 functions that each perform an explicit dispatch on type (for example, real-part calls real-part-rectangular or real-part-polar according to the type of z). Now, we will implement the interface as a single procedure that looks up the combination of the operation name & argument type in the table to find the correct procedure to apply.

Assuming we have two procedures, put and get, for manipulating the operation-and-type table:

(put <op> <type> <item>) installs the <item> in the table, indexed by <op> and <type>.
(get <op> <type>) looks up the <op>, <type> entry in the table and returns the item found there. If no item is found, get returns false.

put and get can be implemented with hash table:

(define table (make-hash-table))

(define (put op type item)
  (hash-set! table (list op type) item))
(define (get op type)
  (hash-ref table (list op type)))

The two representations can now be installed with:

(define (install-rectangular-package)
  ;; internal procedures
  (define (real-part z) (car z))
  (define (imag-part z) (cdr z))
  (define (make-from-real-imag x y) (cons x y))
  (define (magnitude z)
    (sqrt (+ (square (real-part z))
             (square (imag-part z)))))
  (define (angle z)
    (atan (imag-part z) (real-part z)))
  (define (make-from-mag-ang r a)
    (cons (* r (cos a)) (* r (sin a))))

  ;; interface to the rest of the system
  (define (tag x) (attach-tag 'rectangular x))
  (put 'real-part '(rectangular) real-part) ; [1]
  (put 'imag-part '(rectangular) imag-part)
  (put 'magnitude '(rectangular) magnitude)
  (put 'angle '(rectangular) angle)
  (put 'make-from-real-imag 'rectangular    ; [2]
       (lambda (x y) (tag (make-from-real-imag x y))))
  (put 'make-from-mag-ang 'rectangular
       (lambda (r a) (tag (make-from-mag-ang r a))))
  'done)

(define (install-polar-package)
  ;; internal procedures
  (define (magnitude z) (car z))
  (define (angle z) (cdr z))
  (define (make-from-mag-ang r a) (cons r a))
  (define (real-part z) (* (magnitude z) (cos (angle z))))
  (define (imag-part z) (* (magnitude z) (sin (angle z))))
  (define (make-from-real-imag x y)
    (cons (sqrt (+ (square x) (square y)))
          (atan y x)))

  ;; interface to the rest of the system
  (define (tag x) (attach-tag 'polar x))
  (put 'real-part '(polar) real-part)
  (put 'imag-part '(polar) imag-part)
  (put 'magnitude '(polar) magnitude)
  (put 'angle '(polar) angle)
  (put 'make-from-real-imag 'polar
       (lambda (x y) (tag (make-from-real-imag x y))))
  (put 'make-from-mag-ang 'polar
       (lambda (r a) (tag (make-from-mag-ang r a))))
  'done)

Note that for constructors [2], since the result is only of one type, the tag is a symbol. However, for other procedures such as real-part [1], they can have arguments of different types, so a list of symbol is used as tag.

The complex-arithmetic selectors access the table by means of a general "operation" procedure called apply-generic, which applies a generic operation to some arguments. apply-generic looks in the table under the name of the operation and the types of the arguments and applies the resulting procedure if one is present:

(define (apply-generic op . args)
  (let ((type-tags (map type-tag args))) ; type tag of each argument
    (let ((proc (get op type-tags)))     ; get procedure in table
      (if proc
          (apply proc (map contents args))
          (error "No method for these types: APPLY-GENERIC"
                 (list op type-tags))))))

Using apply-generic, we can define generic selectors and the constructors as follows:

(define (real-part z) (apply-generic 'real-part z))
(define (imag-part z) (apply-generic 'imag-part z))
(define (magnitude z) (apply-generic 'magnitude z))
(define (angle z) (apply-generic 'angle z))

(define (make-from-real-imag x y)
  ((get 'make-from-real-imag 'rectangular) x y))
(define (make-from-mag-ang r a)
  ((get 'make-from-mag-ang 'polar) r a))

11.5. Ex 2.76 — a conclusion

As a large system with generic operations evolves, new types of data objects or new operations may be needed. For each of the three strategies—generic operations with explicit dispatch, data-directed style, and message-passing-style—describe the changes that must be made to a system in order to add new types or new operations. Which organization would be most appropriate for a system in which new types must often be added? Which would be most appropriate for a system in which new operations must often be added?

Explicit dispatch allows to add new operations without changing already written code.
Message-passing allows to add new types without changing already written code.
Data-directed approach allows to add new types and new operations just by adding new entries in the operation-and-type table.

12. Symbolic differentiation revisited

From Ex 2.73.

Recall the deriv procedure in symbolic differentiation:

(define (deriv exp var)
  (cond [(constant? exp var) 0]
        [(same-var? exp var) 1]
        [(sum? exp)
         (make-sum (deriv (a1 exp) var)
                   (deriv (a2 exp) var))]
        [(product? exp)
         (make-sum (make-product (m1 exp) (deriv (m2 exp) var))
                   (make-product (m2 exp) (deriv (m1 exp) var)))]))

We can regard this program as performing a dispatch on the type of the expression to be differentiated. In this situation the "type tag" of the datum is the algebraic operator symbol (such as +) and the operation being performed is deriv. We can transform this program into data-directed style by rewriting the basic derivative procedure as

(define (deriv exp var)
  (cond [(constant? exp var) 0]
        [(save-var? exp var) 1]
        [else ((get 'deriv (operator exp))
               (operands exp) var)]))
(define (operator exp) (car exp))
(define (operands exp) (cdr exp))

Now the complete code:

(define (atom? exp)
  (not (pair? exp)))

(define (constant? exp var)
  ;; whether the expression (exp) is a constant
  ;; with respect to the variable (var)
  (and [atom? exp]
       [not (eq? exp var)]))

(define (same-var? exp var)
  (and [atom? exp]
       [eq? exp var]))

(define put '())
(define get '())
(let ([table (make-hash-table)])        ; hide `table' from other functions
  (set! put
        (lambda (op type item)
          (hash-set! table (list op type) item)))
  (set! get
        (lambda (op type)
          (hash-ref table (list op type)))))

(define (install-symbolic-deriv-package)
  ;; same as in deriv.scm
  (define (make-sum a1 a2)
    (cond [(and (number? a1) (number? a2)) (+ a1 a2)]
          [(and (number? a1) (zero? a1)) a2]
          [(and (number? a2) (zero? a2)) a1]
          [else (list '+ a1 a2)]))

  (define (a1 exp) (cadr exp))
  (define (a2 exp) (caddr exp))

  (define (make-product m1 m2)
    (cond [(and (number? m1) (number? m2)) (* m1 m2)]
          [(and (number? m1) (= m1 1)) m2]
          [(and (number? m2) (= m2 1)) m1]
          [(or (and (number? m1) (zero? m1))
               (and (number? m2) (zero? m2))) 0]
          [else (list '* m1 m2)]))

  (define (m1 exp) (cadr exp))
  (define (m2 exp) (caddr exp))

  ;; deriv-sum & deriv-product
  (define (deriv-sum exp var)
    (make-sum (deriv (a1 exp) var)
              (deriv (a2 exp) var)))

  (define (deriv-product exp var)
    (make-sum (make-product (m1 exp) (deriv (m2 exp) var))
              (make-product (m2 exp) (deriv (m1 exp) var))))

  (put 'deriv '+ deriv-sum)
  (put 'deriv '* deriv-product)

  'done)

(install-symbolic-deriv-package)

(define (operator exp) (car exp))
(define (operands exp) (cdr exp))

(define (deriv exp var)
  (cond [(constant? exp var) 0]
        [(same-var? exp var) 1]
        [else ((get 'deriv (operator exp))
               exp var)]))

(define foo '(+ (* a (* x x))           ; ax^2 + bx + c
                (+ (* b x)
                   c)))

(deriv foo 'x)                          ; (+ (* a (+ x x)) b)

13. Exercises

13.1. Ex 2.6 — Church numerals

In case representing pairs as procedures wasn't mind-boggling enough, consider that, in a language that can manipulate procedures, we can get by without numbers (at least insofar as non-negative integers are concerned) by implementing 0 and the operation of adding 1 as
(define zero (lambda (f) (lambda (x) x)))

(define (add-1 n) (lambda (f) (lambda (x) (f ((n f) x)))))
This representation is known as Church numerals, after its inventor, Alonzo Church, the logician who invented the calculus.

Define one and two directly (not in terms of zero and add-1). (Hint: Use substitution to evaluate (add-1 zero)). Give a direct definition of the addition procedure + (not in terms of repeated application of add-1).

Recall the two functions compose and repeated from Ex 1.42 and 1.43:

((compose square inc) 6)                ; (square (inc 6)) = 49
((repeated square 2) 5)                 ; (square (square 5)) = 625

A Church number cn (that corresponds to a normal integer n) is a function that takes a one-argument function f, and applies it n times. That is, (cn f) is equivalent to (repeated f n).

First we have zero and add-1:

(define zero
  (λ (f)
    (λ (x)
      x)))                              ; does not apply f

(define (add-1 n)
  (λ (f)
    (λ (x)
      (f ((n f) x)))))

((zero square) 5)                       ; 5
(((add-1 zero) square) 5)               ; 25
(((add-1 (add-1 zero)) square) 5)       ; 625

((repeated square 0) 5)                 ; 5
((repeated square 1) 5)                 ; 25
((repeated square 2) 5)                 ; 625

one and two become quite easy now that we know what Church numbers do:

(define one
  (λ (f)
    (λ (x)
      (f x))))                          ; apply 1 time

(define two
  (λ (f)
    (λ (x)
      (f (f x)))))                      ; apply 2 times

((one square) 5)                        ; 25
((two square) 5)                        ; 625

In order to get 3, we can add one and two, and obtain as result something like (f (f (f x))). ((one f) x) is (f x), (two f) is (λ (x) (f (f x))). Make ((one f) x) the argument of (two f), we get:

((two f) ((one f) x))                   ; => (f (f (f x)))

So addition is:

(define (add a b)
  (λ (f)
    (λ (x)
      ((a f) ((b f) x)))))

((two square) ((one square) 5))         ; 390625
(((add one two) square) 5)              ; 390625

One can use these as normal integers:

(define (church->int ch)
  ((ch 1+) 0))

(church->int zero)                      ; 0
(church->int two)                       ; 2
(church->int (add one two))             ; 3

(define three (add one two))
(church->int (add two three))           ; 5

Here's a more concise implementation of add:

(define (add a b)
  ((a add-1) b))

Here (a add-1) essentially transforms add-1 to add-a, a function that adds a to a Church number.

13.2. Ex 2.20 — dotted-tail notation

The procedures +, *, and list take arbitrary numbers of arguments. One way to define such procedures is to use define with dotted-tail notation. In a procedure definition, a parameter list that has a dot before the last parameter name indicates that, when the procedure is called, the initial parameters (if any) will have as values the initial arguments, as usual, but the final parameter's value will be a list of any remaining arguments. For instance, given the definition
(define (f x y . z) <body>)
the procedure f can be called with two or more arguments. If we evaluate
(f 1 2 3 4 5 6)
then in the body of f, x will be 1, y will be 2, and z will be the list (3 4 5 6). Given the definition
(define (g . w) <body>)
the procedure g can be called with zero or more arguments. If we evaluate
(g 1 2 3 4 5 6)
then in the body of g, w will be the list (1 2 3 4 5 6).

Use this notation to write a procedure same-parity that takes one or more integers and returns a list of all the arguments that have the same even-odd parity as the first argument. For example,
(same-parity 1 2 3 4 5 6 7)
(1 3 5 7)

(same-parity 2 3 4 5 6 7)
(2 4 6)

(define (same-parity first . rest)
  (let ([pred (if (odd? first)
                  odd?
                  even?)])
    (define (iter l)
      (if (null? l)
          '()
          (let ([first (car l)]
                [rest  (cdr l)])
            (if (pred first)
                (cons first (iter rest))
                (iter rest)))))
    (cons first
          (iter rest))))

;;; old solution
(define (same-parity first . rest)
  (let ((yes? (if (odd? first)
                  odd?
                  even?)))
    (define (iter l res)
      (cond ((null? l) res)
            ((yes? (car l)) (iter (cdr l) (cons (car l) res)))
            (else (iter (cdr l) res))))
    (cons first
          (reverse (iter rest '())))))

13.3. Ex 2.27 — deep reverse

Modify your reverse procedure of Exercise 2.18 to produce a deep-reverse procedure that takes a list as argument and returns as its value the list with its elements reversed and with all sub-lists deep-reversed as well. For example,
(define x (list (list 1 2) (list 3 4))) ; ((1 2) (3 4))
(reverse x)                             ; ((3 4) (1 2))
(deep-reverse x)                        ; ((4 3) (2 1))

(define (deep-reverse tree)
  (if (atom? tree)
      tree
      (reverse (map deep-reverse tree))))

13.4. Ex 2.28 — fringe

Write a procedure fringe that takes as argument a tree (represented as a list) and returns a list whose elements are all the leaves of the tree arranged in left-to-right order. For example,
(define x (list (list 1 2) (list 3 4)))
(fringe x)                              ; (1 2 3 4)
(fringe (list x x))                     ; (1 2 3 4 1 2 3 4)

(define (fringe tree)
  (cond [(null? tree) '()]
        [(atom? tree) (list tree)]
        [else (append (fringe (car tree))
                      (fringe (cdr tree)))]))

(define (fringe tree)
  (define (iter tree res)
    (cond [(null? tree) res]
          [(atom? tree) (cons tree res)]
          [else (iter (car tree)
                      (iter (cdr tree) res))]))
  (iter tree '()))

13.5. Ex 2.32 — subset

We can represent a set as a list of distinct elements, and we can represent the set of all subsets of the set as a list of lists. For example, if the set is (1 2 3), then the set of all subsets is (() (3) (2) (2 3) (1) (1 3) (1 2) (1 2 3)). Complete the following definition of a procedure that generates the set of subsets of a set and give a clear explanation of why it works:
(define (subsets s)
  (if (null? s)
      (list nil)
      (let ((rest (subsets (cdr s))))
        (append rest (map <??> rest)))))

(define (subsets s)
  (if (null? s)
      (list '())
      (let ([rest (subsets (cdr s))])
        (append rest
                (map (lambda (x)
                       (cons (car s) x))
                     rest)))))

13.6. Ex 2.35 — counting leaves

Redefine count-leaves from Section 2.2.2 as an accumulation.

(define (count-leaves tree)
  (accumulate + 0
              (map (lambda (tree)
                     (if (atom? tree)
                         1
                         (count-leaves tree)))
                   tree)))

This seems fine, but it will count the empty list as a leaf:

(count-leaves '(1 2 (3 (4 5) 6) 7))     ; 7
(count-leaves '(1 2 (3 (4 5) 6) 7 ()))  ; 8

Take into consideration the empty list '():

(define (count-leaves tree)
  (accumulate + 0
              (map (lambda (tree)
                     (cond [(null? tree) 0]
                           [(atom? tree) 1]
                           [else (count-leaves tree)]))
                   tree)))

(count-leaves '(1 2 (3 (4 5) 6) 7))     ; 7
(count-leaves '(1 2 (3 (4 5) 6) 7 ()))  ; 7

Author	thebesttv
Created	2021-07-04 09:17
Modified	2023-05-18 11:31
Generated	2024-06-11 02:39
Version	Emacs 29.3 (Org mode 9.6.15)
Raw	ch2.org